در این آموزش کوتاه میخواهیم تبدیل فوریه سریع یا FFT را معرفی کنیم. به بیان ریاضی کاری که این ابزار انجام میدهد تجزیه یک سیگنال به عوامل سازنده آن سیگنال است. عوامل سازنده در تبدیل فوریه سریع سینوسیها با فرکانسهای مختلف هستند. البته تبدیلات دیگری مانند تبدیل موجک وجود دارند که عوامل سازنده در آنها متفاوت است و در مطلب جداگانهای به آن خواهیم پرداخت.
خیلی اوقات پیش میاد که در کاربردهای تحقیقاتی و دانشگاهی دنبال این هستیم که ببینیم در یک سیگنال چه مولفههای فرکانسی مهمی وجود دارد. برای مثال، با آنالیز سیگنال ارتعاش یک موتور الکتریکی میتوان وجود عیب در بخشهای مختلف آن را شناسایی کرد. و یا از طریق آنالیز سیگنال الکتروکاردیوگرام یا ECG میتوان خیلی از بیماریهای قلبی و ناهنجاریهای مرتبط با آن را شناسایی کرد. تبدیل فوریه سریع یکی از ابزارهای خیلی خیلی مهم و کاربردی برای آنالیز سیگنالهای واقعی و صنعتی است. در ادامه میخواهم چگونگی محاسبه تبدیل فوریه یک سیگنال را در نرمافزار قدرتمند متلب را آموزش بدهم.
مثال تبدیل فوریه سریع یا FFT
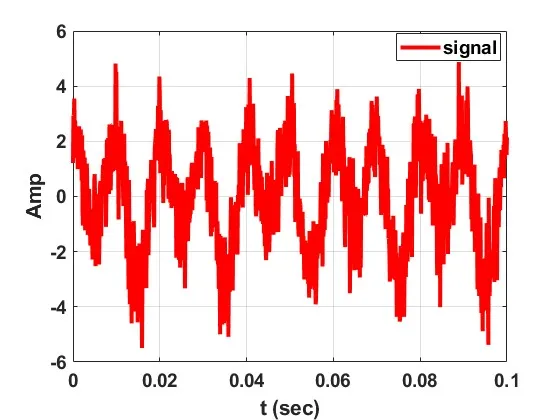
فرض کنید در یک کاربرد صنعتی سیگنال شکل زیر با استفاده از کارت دادهبرداری DAQ ثبت شده است و میخواهیم عناصر سازنده آن را تشخیص دهیم. در محاسبه تبدیل فوریه سریع FFT باید فرکانس نمونهبرداری کاملاً مشخص باشد. فرکانس نمونهبرداری یعنی اینکه در هر ثانیه چند نمونه ثبت شده است و یا ثبت هر نمونه چند ثانیه طول کشیده است. مشخص است که از روی شکل ظاهری سیگنال نمیتوان فرکانسهای موجود در آن را تشخیص داد. شاید اگر سیگنال نویز کمی داشت میتوانستیم این کار را انجام دهیم. ولی در کاربردهای صنعتی عموماً نویز شدیدی وجود دارند و شکل سیگنالها تقریباً به همین صورت است.
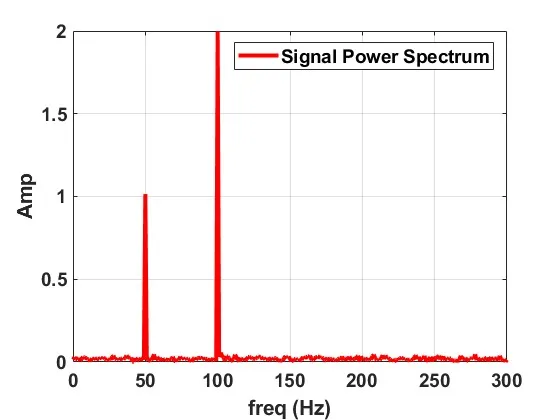
در شکل زیر تبدیل فوریه این سیگنال نشان داده شده است. با توجه به این شکل مشخص است که درصد خیلی بالایی (۹۹ درصد!) سیگنال شکل بالا از دو فرکانس 50 و 100 هرتز تشکیل شده است که نویز تصادفی هم به آن اضافه شده است. بنابراین، با توجه به این مثال ساده، میتوان قدرت تبدیل فوریه سریع را درک کرد. با استفاده از FFT میتوان محتوای فرکانسی سیگنالهای صنعتی را استخراج نمود و از طریق آنها میتوان اطلاعات سودمندی را هم به دست آورد.
با استفاده از برنامه زیر در نرمافزار متلب میتوانید سیگنالهای دلخواه و تبدیل فوریه آنها را رسم کنید. اگر سیگنال عملی دارید که در یک فایل CSV ذخیره شده است به راحتی با دستور csvread یا fileread میتوانید آنها را در متلب فراخوانی کنید و به جای آرایه signal در برنامه زیر استفاده کنید تا تبدیل فوریه سریع FFT آن رسم شود. نکته آخر این است که از نظر ریاضی تبدیل فوریه سریع همانند سری فوریه زمان گسسته است و فرض میکند که سیگنالی که ثبت شده با همان طول ثبتشده متناوب است. به عبارت دیگر، اگر هزار داده ثبت شده است، تبدیل فوریه فرض میکند که سیگنال دارای دوره تناوب هزار نمونه است و سپس تبدیل فوریه در حقیقت همان ضرایب سری فوریه گسسته سیگنال است.
مشکلی که در این فرض ایجاد می شود این است که اگر دادههای اول و آخر با هم برابر نباشند در سیگنال فرض شده توسط تبدیل فوریه سریع ناپیوستگی وجود دارد. به همین دلیل علاوه بر پیکهای فرکانسی اصلی سیگنال یک سری پیکهای جعلی (طبف نشتی) هم ایجاد میشوند. برای رع این مشکل قبل از وارد کردن سیگنال در دستور FFT سیگنال ثبتشده در یک پنجره ضرب میشود. پنجرههای در حقیقت وزندهی به نمونههای ثبتشده هستند و همیشه وزن نمونه اول و آخر صفر است. در نتیجه اگر پنجره در سیگنال ضرب شود نمونه اول و آخر همیشه صفر میشوند و دیگر طیف جعلی ایجاد نمیشود. در معروفترین پنجرههای استفادهشده در تبدیل فوریه سریع میتوان به پنجره Hamming و Hanning اشاره کرد.
کد متلب MATLAB تبدیل فوریه سریع FFT
clc
clear;
close all;
warning off
%% Plot FFT Using Matlab
Fs = 10e3; % Sampling Rate in Hz
Ts = 1/Fs; % Sampling Time
Tf = 1; % Data Recording Length
t = 0:Ts:Tf ; t = t’ ;
signal = sin(2*pi*50*t) + 2*cos(2*pi*100*t) ; % define signal
signal = signal + randn(size(signal)) ; % add noise
L = numel(signal) ; % number of recorded data
signalFFT = fft(signal .* hamming(L));
P2 = abs(signalFFT/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
freq = Fs*(0:(L/2))/L; % frequency range
Fig = figure(1);
Fig.WindowState = ‘normal’ ;
Fig.Color = [1 1 1] ;
plot(t , signal , ‘r’ , ‘linewidth’ , 3 );
xlabel(‘t (sec)’ , ‘FontSize’ , 14, ‘FontWeight’,’bold’);
ylabel(‘Amp’ , ‘FontSize’ , 14, ‘FontWeight’,’bold’);
title(‘Time Domain Signal’ , ‘FontSize’ , 14, ‘FontWeight’,’bold’);
fig = gca ;
fig.FontSize = 14 ;
fig.FontWeight = ‘B’ ;
grid on ;
xlim([0 0.1])
Fig = figure(2);
Fig.WindowState = ‘normal’ ;
Fig.Color = [1 1 1] ;
plot(freq , P1 , ‘r’ , ‘linewidth’ , 3 );
xlabel(‘freq (Hz)’ , ‘FontSize’ , 14, ‘FontWeight’,’bold’);
ylabel(‘Amp’ , ‘FontSize’ , 14, ‘FontWeight’,’bold’);
title(‘Signal Power Spectrum’ , ‘FontSize’ , 14, ‘FontWeight’,’bold’);
fig = gca ;
fig.FontSize = 14 ;
fig.FontWeight = ‘B’ ;
grid on ;
xlim([0 300])
پیروز و شاد و تندرست باشید.